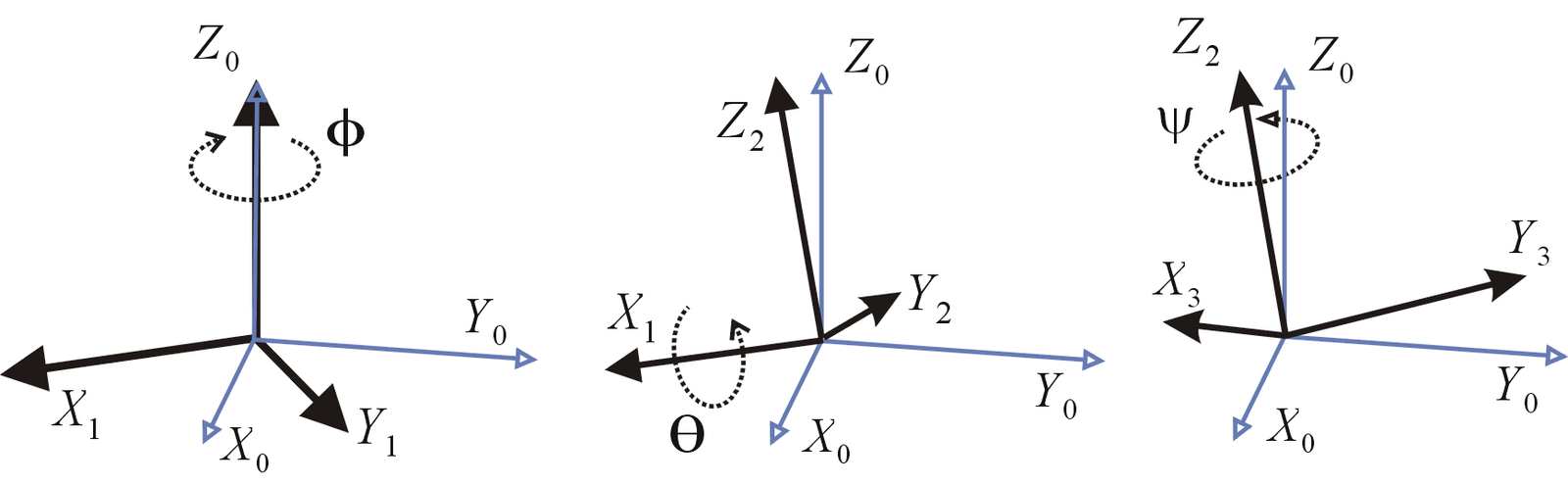
Rotation: Focus angles d'Euler

• Trois rotations consécutives autour d'axes fixes orthogonaux.

• Représentation sous forme de multiplication de matrices

• \(R_x=\left(\begin{array}{ccc}1 & 0 & 0 \\ 0 & \cos(\alpha) & \sin(\alpha) \\ 0 & -\sin \alpha) & \cos(\alpha)\end{array}\right) \;\;\) \(R_y= \left( \begin{array}{ccc} \cos(\beta) & 0 & \sin(\beta) \\ 0 & 1 & 0 \\ -\sin(\beta) & 0 & \cos(\beta) \end{array} \right) \;\;\) \(R_z= \left( \begin{array}{ccc} \cos(\gamma) & \sin(\gamma) & 0 \\-\sin(\gamma) & \cos(\gamma) & 0 \\0 & 0 & 1 \end{array} \right) \)

• Conventions multiples pour les angles d'Euler
• • - Proper Euler : z-x-z', x-y-x', y-z-y', ...
  • - Trait-Bryan : x-y-z, z-y-x, x-z-y, ...
  • Attention lors de l'export/import/parsing entre différent logiciels

• Pro

• • - Composition de rotations autour d'axes fixes
  • - Paramètres compréhensibles (3 dof)
  • - Les animateurs peuvent interagir avec les courbes angulaires
  • - Largement utilisé en robotique